Η ταυτότητα του Όιλερ (Euler's identity) στη μαθηματική ανάλυση, είναι η εξίσωση
όπου
 είναι ο αριθμός του Όιλερ, η βάση των φυσικών λογαρίθμων,
είναι ο αριθμός του Όιλερ, η βάση των φυσικών λογαρίθμων,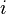 είναι ο φανταστικός αριθμός, ένας μιγαδικός αριθμός του οποίου το τετράγωνο ισούται με μείον ένα , και
είναι ο φανταστικός αριθμός, ένας μιγαδικός αριθμός του οποίου το τετράγωνο ισούται με μείον ένα , και ο λόγος του μήκους της περιφέρειας ενός κύκλου προς τη διάμετρό του.
ο λόγος του μήκους της περιφέρειας ενός κύκλου προς τη διάμετρό του.
Πήρε το όνομά της από τον Λέοναρντ Όιλερ και μερικές φορές είναι γνωστή και ως εξίσωση του Όιλερ.
Απόδειξη
Η ταυτότητα είναι μια ειδική περίπτωση της εξίσωσης του Όιλερ, σύμφωνα με την οποία
για κάθε πραγματικό αριθμό x. (οι μονάδες δίνονται σε ακτίνια.) Συγκεκριμένα, αν
τότε
Αφού
Συνεπώς,
που δίνει την ταυτότητα

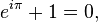


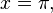



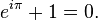
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου